1. týden
- Hamiltonův princip
- Eulerova-Lagrangeova rovnice
Pohyb tělesa
Sbírka příkladů, př. 1.
Uvažujte pohyb částice o hmotnosti m po svislé přímce v homogenním tíhovém poli. Poloha částice je popsána funkcí x(t), přičemž v počátečním čase t = 0 a koncovém čase t = T je poloha částice x(0) = x(T) = 0. Předpokládejte, že funkce x(t) má tvar:
a) x(t) = a + bt + ct2,
b) x(t) = a + bsin(ct),
kde a,b,c jsou parametry. Ze znalosti výše uvedených podmínek vyjádřete parametry a,c pomocí času T a zbývajícího parametru b. Vypočtěte akci a určete hodnotu b0 parametru b, pro niž je hodnota akce minimální. Srovnejte minimální hodnoty akce odpovídající dvěma předpokládaným trajektoriím. Dále určete zrychlení částice v obecném čase t pro parametr b0. Co z toho lze usoudit?

Volná částice
Poznámky k přednáškám, str. 3, odvození charakteru pohybu přímo z principu nejmenší akce.
-
Uvažujme volnou částici (potenciální energie je všude nulová, na částici nepůsobí žádné síly). Předpokládejme, že počáteční a koncový bod splývají. Jakému pohybu odpovídá nejmenší akce?
-
Uvažujme opět volnou částici, tentokrát ale počáteční a koncový bod nesplývají.
Snellův zákon
Fermatův princip nejmenšího času

Volný pád
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ volného pádu. Řešte také pohybové rovnice.

Volná částice 2
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ pohybu volné částice.

Těleso na pružině
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ tělesa na pružině. Vyřešte také pohybovou rovnici.

2. týden
- Eulerova-Lagrangeova rovnice
- Integrál energie
Matematické kyvadlo
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ matematického kyvadla. Nalezněte zobecněné souřadnice tak, aby byly vazby automaticky splněny. Vypočtěte integrál energie.

Jednoduchý kladkostroj
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ jednoduchého kladkostroje na obrázku. Vypočtěte zrychlení.

Válec na pružině
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ válce na pružině dle obrázku. Určete zrychlení válce a srovnejte s klasickým řešením.

Těleso na válci
Sbírka příkladu, př. 10.
Těleso o hmotnosti m je spojené s lanem, které se bez tření odvinuje z kladky o hmotnosti M a poloměru R. Tíhová síla působí vertikálně směrem dolů. Určete zrychlení tělesa.

Válec na nakloněné rovině
Sbírka příkladu, př. 13.
Válec o hmotnosti m a poloměru R se valí bez klouzání dolů po nakloněné rovině s úhlem sklonu α. Určete zrychlení válce.

Koule vs válec
Sbírka příkladu, př. 14.
Válec o poloměru R1 a hustotě ρ1 a koule o poloměru R2 a hustotě ρ2 se valí po téže nakloněné rovině s úhlem sklonu α. Které z obou těles dosáhne většího zrychlení? Jak závisí odpověď na hodnotách ρ1,2 a R1,2 ?
Tělesa na nakloněné rovině
Sbírka příkladu, př. 15.
Určete zrychlení tělesa o hmotnosti m1 z obrázku. Nakloněná rovina je v klidu, kladku považujte za nehmotnou, tření neuvažujte.

Blok na klínu
Sbírka příkladu, př. 16.
Blok o hmotnosti m klouže bez tření po tělese ve tvaru nakloněné roviny o hmotnosti M, které se může pohybovat v horizontální rovině také bez tření (viz obrázek). Určete pohybové rovnice a zrychlení bloku a nakloněné roviny.

3. týden
- Integrál energie
- Zobecněná hybnost
Dvě tělesa na klínu
Sbírka příkladu, př. 17.
Určete zrychlení klínu o hmotnosti M z obrázku. Všechna tření zanedbejte, kladku považujte za nehmotnou.

Dvě tělesa spojená pružinou
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ dvou těles spojených pružinou dle obrázku. Určete zrychlení těles a módy kmitání.

Dvě tělesa spojená pružinami
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ dvou těles spojených pružinami dle obrázku. Určete zrychlení těles a módy kmitání.

Rotující těleso na pružině
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ rotujícího tělesa na pružině s jedním stupněm volnosti. Určete zrychlení tělesa.

4. týden
- Integrál energie
- Zobecněná hybnost
Kyvaldo na pružině
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ kyvalda na pružině s dvěma stupni volnosti. Určete pohybové rovnice. Vypočtěte zobecněnou energii i hybnost.

Kyvadlo na tělesu
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ kyvalda na tělesu. Určete pohybové rovnice. Vypočtěte zobecněnou energii i hybnost.

Kyvadlo na tělesu s pružinou
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ kyvalda na tělesu s pružinou dle obrázku. Určete pohybové rovnice. Vypočtěte zobecněnou energii i hybnost.

Wattův regulátor
Pomocí Eulerovy-Lagrangeovy rovnice řešte případ Wattova odstředivého regulátoru dle obrázku. Určete pohybovou rovnici a vyjádřete úhel φ jako funkci úhlové rychlosti Ω.

5. týden
- Zobecněná hybnost
- Hamiltonovy rovnice
Jednoznačnost Lagrangeovy funkce
Poznámky k přednáškám, str. 6, otázka jednoznačnosti Lagrangeovy funkce. Řešte daný příklad.
Integrace pobybových rovnic
Poznámky k přednáškám, str. 12–13, integrace (řešení) pohybových rovnic v jedné dimenzi. Odvoďte rovnici 49 a řešte případ volného pádu.
Problém dvou těles
Poznámky k přednáškám, str. 14. Odvoďte rovnici 56.

Hamiltonovy rovnice
Napište Hamiltonovu funkci volného hmotného bodu v kartézských, sférických a válcových souřadnicích.
Hamiltonovy rovnice
Napište Hamiltonovy kanonické rovnice pro pohyb částice v jedné dimenzi.
Hamiltonovy rovnice
Sestavte Hamiltonovy kanonické rovnice pro pohyb částice ve třech dimenzích.
Hamiltonovy rovnice
Určete Hamiltonovu funkci a rovnice pro matematické kyvadlo.

Hamiltonovy rovnice
Určete Hamiltonovu funkci a rovnice pro těleso na pružině.

6. týden
První zápočtová práce. Jedná se o 4 příklady z teoretické mechaniky. Pro dosažení zápočtu je nutné získat 60 bodů ze 100.
7. týden
1. říjen, odpadá.
8. týden
- Pružnost
- Tenzor deformace
Tenzor deformace
Spočtěte tenzor deformace v rovině pro následující případy (a to nejen pro malé deformace, ale rovněž velké). Jednotlivé členy interpretujte.
a) u = (Ax, Ay)
b) u = (Ax, 0)
c) u = (Ay, 0)
d) u = (Ay, Ax)
e) u = (-Ay, Ax)
f) u = (x(cosα − 1) − y sinα, x sinα + y(cosα − 1))
9. týden
- Pružnost
- Tenzor napětí
Napětí 1
Obecně určete napětí v rovině definovanou normálovým vektorem (1, 0).
Napětí 2
Obecně určete napětí v rovině definovanou normálovým vektorem (0, 1).
Napětí 3
Obecně určete napětí v rovině definovanou normálovým vektorem (2√2, 2√2).
Napětí 4
Nechť jsou síly působící na deformované těleso rozloženy tak, že problém můžeme považovat za rovinný. V určitém bodě P tělesa je znám tenzor napětí. Určete normálovou a tečnou složku napětí na rovině, která svírá s osou x úhel α.
Píst
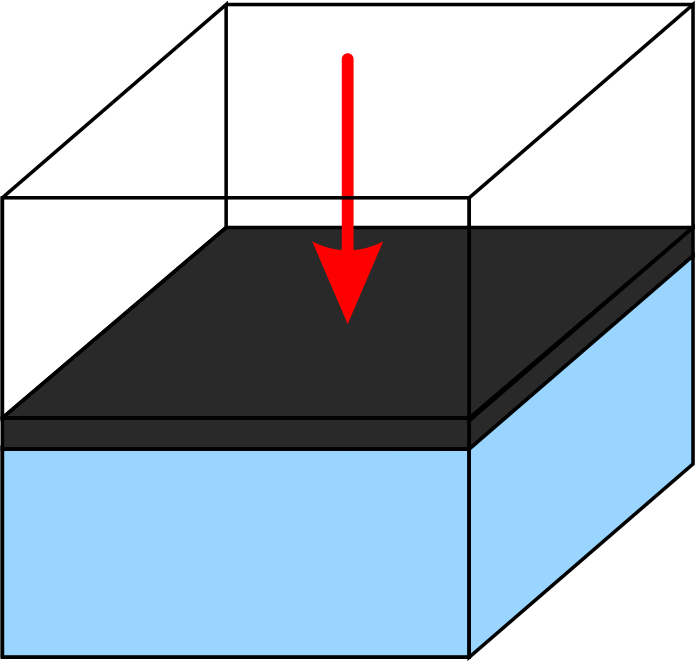
Řešte stlačování tělesa obklopeného pevnými stěnami, kde je těleso uzavřeno v kvádru s pěti pevnými stěnami, šestou ’stěnou’ je pohyblivý píst.
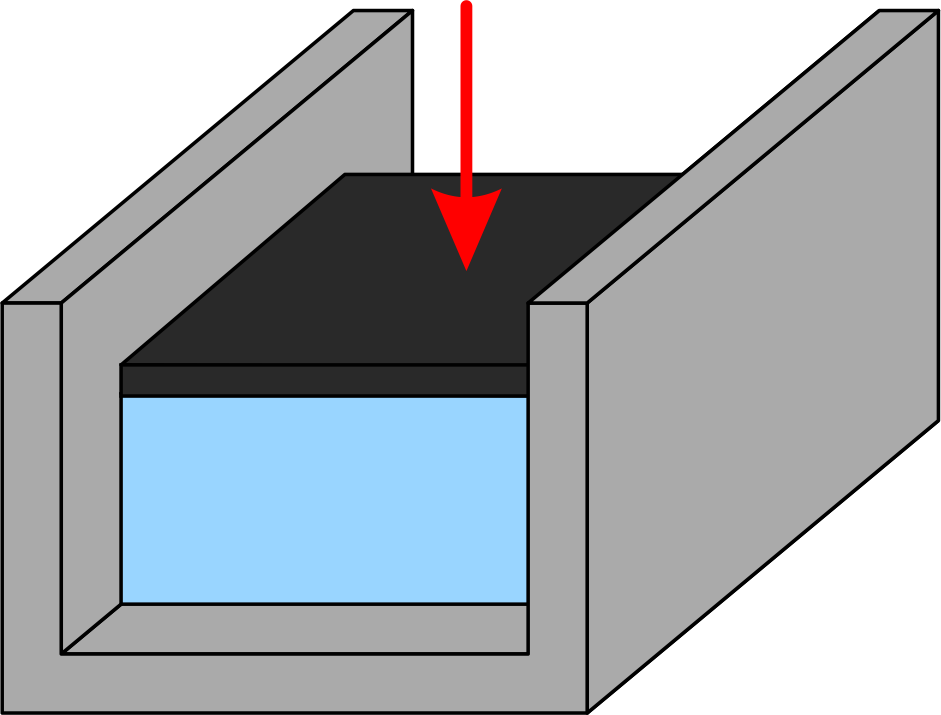
Těleso na traverze
Řešte stlačování tělesa obklopeného pevnými stěnami, kde je těleso uloženo na traverze – profil se třemi pevnými stěnami (dvě boční a spodní stěna). Tělesu, na které tlačíme shora pístem, je tedy umožněno rozpínat se v jedné ose.
Natahování tyče
Řešte případ natahování tyče.
10. týden
- Mechanika tekutin
- Navier-Stokesovy rovnice
Operátor nabla
Vyjádřete gradient skalární a divergenci a rotaci vektorové funkce. Vyjádřete také Laplaceův operátor. Vše v kartezských, válcových a sférických souřadnicích.
Eulerova rovnice
Napište a popište veškeré členy Eulerovy rovnice. Odvoďte zrychlení elementu objemu tekutiny.
Navier-Stokesova rovnice
Napište a popište veškeré členy Navier-Stokesovy rovnice.
Tok hmotnosti
Najděte tok hmotnosti z koule o poloměru R se středem v počátku pro radiální proudění zadané polem rychlosti v = A(x,y,z).
Hydrostatika
Pomocí Eulerovy rovnice řešte případ nepohybující se kapaliny v tíhovém poli.
Rotující kapalina
Pomocí Eulerovy rovnice řešte případ nestlačitelné rotující kapaliny v tíhovém poli.
Bernoulliho rovnice
Užitím Eulerovy rovnice vyjádřete Bernoulliho rovnici.
Rychlost kapaliny
Pomocí Bernoulliho rovnice určete rychlost kapaliny vytékající z nádoby.
11. týden
- Mechanika tekutin
- Navier-Stokesovy rovnice
Proudění v trubce
Řešte případ proudění kapaliny ve válcové trubce o poloměru R2. Popište rychlostní pole. Gravitaci neuvažujte. Jedná se o nestlačitelnou kapalinu s viskozitou. Vypočtěte celkový tok trubkou.

Proudění v souosé trubce
Řešte jak se situace v předchozí úloze změní, když do trubky souose umístíme nekonečný válec o poloměru R1 < R2.

Rotující trubka
Kapalina o dynamické viskozitě η je umístěná mezi dvěma souosými trubkami o poloměrech R1 < R2. Vnější trubka rotuje konstantní rychlostí ω. Popište rychlostní pole v kapalině.

12. týden
- Mechanika tekutin
- Navier-Stokesovy rovnice
Tvar hladiny ideálního víru
Pomocí Eulerovy rovnice nalezněte tvar hladiny pro ideální vír. Rovněž ukažte, že se celková energie částic zachovává. U ideálního víru proudnice tvoří kružnice kolmé na osu víru (vírovou čáru), jejichž středy leží na vírové čáře.

Tvar hladiny rotující kapaliny
Pomocí Eulerovy rovnice nalezněte tvar volné hladiny kapaliny rotující jako celek.

Proudění v řece
Řešte proudění v řece. Toto proudění můžeme aproximovat viskózní kapalinou proudící po nakloněné rovině se sklonem α. Určete závislost rychlosti kapaliny na vzdálenosti od nakloněné roviny. Jaký je celkový objemový tok?

13. týden
Druhá zápočtová práce. Jedná se o 3 příklady z mechaniky kontinua. Pro dosažení zápočtu je nutné získat 60 bodů ze 100.